|
|
|
Anatolii Vladimirovich Skorokhod, 1930 – 2011
Igor Vajda, Principal Researcher at the Institute of Information Theory and Automation (ÚTIA) of the Academy of Sciences of the Czech Republic in Prague, and a leading figure in the field of information-theoretic statistical inference, passed away unexpectedly on May 2, 2010. He was born on October 20, 1942, in Martin, Czechoslovakia. After attending elementary and secondary school in Slovakia, he graduated in mathematics at Czech Technical University (CTU) in Prague in 1965, and received Candidate of Science and Doctor of Science degrees from Charles University in 1968 and 1990, respectively, with specializations in probability, statistics and mathematical informatics. He had been a key researcher at ÚTIA since 1965 and held a teaching position at CTU since 1969. For many years he was head of the Department of Stochastic Informatics of ÚTIA and served on the Scientific Boards of both ÚTIA and the Faculty of Electrical Engineering of CTU.
Although Igor Vajda had little opportunity to travel before 1989, apart from a one-year stay in Moscow in the 1960s and a two-year teaching appointment in Cairo in the 1970s, he developed many contacts abroad, especially in Western Europe, after the political changeover in Czechoslovakia in 1989. Since 1991 he intensively cooperated in research with colleagues in Austria, Belgium, Denmark, France, Germany, Hungary, Spain, and the USA.
|
|
|
Igor Vajda |
Igor Vajda recognized early the meaning of different types of distances
between distributions in information theory and mathematical statistics. One of
his major research directions was the investigation of ƒ-divergences
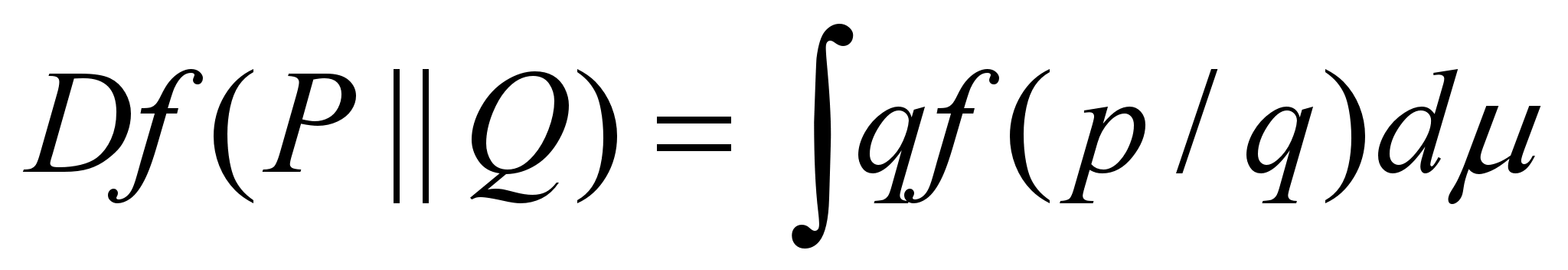
of
distributions P and Q with densities p = dP/dµ and q =dQ/dµ, and their
statistical applications. In early papers he studied the relations between
ƒ-divergences and variational distance, the approximation, monotonicity,
topological properties of ƒ-divergences and their minimization under
constraints.
A first systematic theory of ƒ-divergences was presented in the book Convex Statistical Distances by F. Liese and I. Vajda (Teubner, 1986), with applications to hypothesis testing, minimum distance estimation, and random processes. Igor Vajda's book Theory of Statistical Inference and Information (Kluwer, 1989) (a first version was published in Slovak language in 1982) provides a comprehensive treatment of the theory of statistical inference and information. This book is unique in the field, contains a wealth of research results and has become an indispensable source of reference for researchers in the domain.
Igor Vajda used special ƒ-divergences to generalize the Cramer-Rao bound and
the theorems of Chernoff and Stein. The extension of the likelihood ratio
statistic to divergence-based statistics for testing composite hypotheses was
the subject of many papers of which he was the author or a co-author. In order
to compare the empirical distribution
with the theoretical distribution
from a
parametric model, one must turn to a sequence of partitions of the sample space.
Igor Vajda and co-authors characterized the suitable speed of refining, and
studied sequences of partitions generated by the quantile function.
Another, closely related research topic of Igor Vajda was the
divergence-based estimation and testing in mathematical statistics. He used the
distance 
between the empirical distribution
and the true distribution
to
introduce the minimum divergence estimator
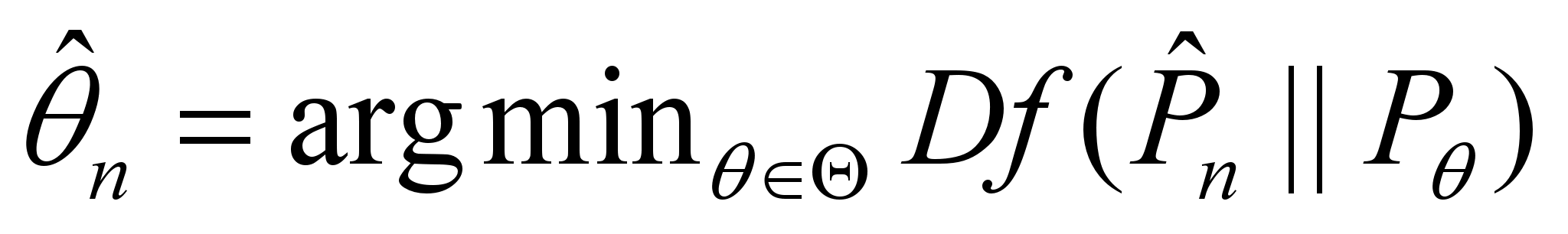
and to construct the statistic
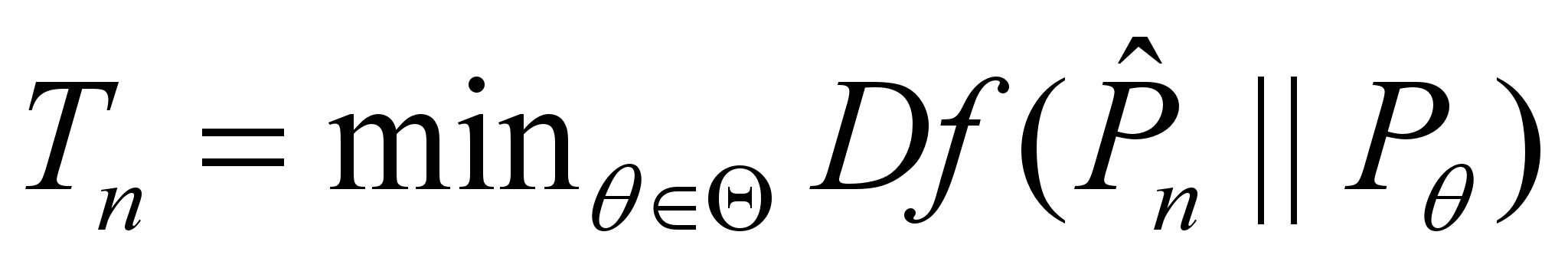
for
testing a parametric hypothesis and for goodness of fit tests. He and co-authors
showed that ƒ-divergence based estimates have similar properties as the maximum
likelihood estimator. These results, as well as the efficiency in the Pitman and
Bahadur sense and large deviation results on tests based on
Tn, were the subject
of many papers of which Igor was the author or a co-author. Igor Vajda noticed
the importance of the Barron distribution estimator, originally introduced for
the consistent nonparametric estimation of an unknown probability distribution
in the sense of information divergence and variational distance. In a series of
papers, he and co-authors proved many other results concerning this estimator,
such as consistency in chi-square divergence, and applied it to density
estimation and parametric minimum distance point estimation.
Starting 2001, Igor Vajda developed a general theory of goodness-of-fit tests based on spacings from the viewpoint of disparity statistics. In joint work he showed that essentially all spacings-based statistics are asymptotically equivalent to a disparity statistic and proved limit laws for this class of statistics, with special attention to power divergence statistics, thereby obtaining closed-form expressions for the asymptotic parameters of these power divergence spacings-based statistics.
In recent papers Igor Vajda studied the Bregman distance, which provides the flexibility to find a compromise between efficiency and robustness of estimators based on it.
He also worked in applied areas such as the statistical analysis of optimal investments, financial mathematics, biostatistics, and stochastic systems and networks.
Igor Vajda was a passionate researcher, always exploring new ideas. His results were respected by the scientific community and influenced the research orientation of many of his younger colleagues. In his scientific work he continued the traditional Prague school of information theory, which dates back to the early 1950s. Igor was an author or co-author of four monographs and more than 100 publications in renowned international journals. He had over 300 officially registered citations.
Igor Vajda's work was awarded, among other distinctions, the Prize of the Czech Academy of Sciences, the Jacob Wolfowitz Prize, the Medal of the Merits of the First Degree from the Faculty of Nuclear and Physical Engineering of CTU and several Annual Prizes awarded by the Director of ÚTIA for the best paper of the year. In November 2010, at a special Colloquium held in his memory at Prague, Igor Vajda was honored posthumously with the Bolzano Medal from the Academy of Sciences of the Czech Republic. The high quality of his scientific results and the intensity of his international cooperation are expressed by the fact that since 1991 Igor Vajda obtained six research grants from the Czech National Grant Agency, one from the European Union (Copernicus), and one from the NSF of the USA. He participated as a co-investigator in several other grants. Since 1990 Igor Vajda was a Member and since 2001 a Fellow of the IEEE. He was a visiting professor at Katholieke Universiteit Leuven, Complutense Universidad Madrid, Université de Montpellier, and M. Hérnandez Universidad, Alicante.
Igor Vajda supervised many diploma projects and guided several PhD students both at home and abroad. He was a co-editor of the journals Kybernetika, Problems of Control and Information Theory, Applications of Mathematics, Statistics and Decisions, Revista Matematica Complutense, Journal of Statistical Planning and Inference, and Test.
Igor Vajda loved his native land Slovakia and visited it regularly throughout his life. He is survived by his wife Zdenka, his two daughters Tereza and Veronika, and four grandchildren. Igor Vajda was a man of many ambitions and achieved a lot in his life. He worked tirelessly and inspired many. He enjoyed working with others. With him we lost a great friend and fine colleague. We all owe him much, miss him, and will honor his memory.
Martin Janzura, ÚTIA, Prague
Friedrich Liese, Univ. of Rostock
Edward van der Meulen, K. U. Leuven
Note: This obituary is an abridged and slightly modified version of the one which appeared in the April/May 2011 issue of the IMS bulletin.
Professor Anatolii Vladimirovich Skorokhod, who had been a member of the Department of Statistics and Probability at Michigan State University since 1994, died on January 3, 2011. His contributions in 230 published works are too numerous to cover in a short review. I try to enumerate his work with major impact in the subject.
Skorokhod decided to specialize in Probability and carried out investigations under the influence of B.V. Gnedenko and I.I. Gikhman at Kiev. In 1953, he was taken to Moscow State University by Gnedenko. He was advised by Professor A.N. Kolmogorov to work under the guidance of Professor E.B. Dynkin.
Skorokhod’s first major work as a postgraduate researcher was to discover a topology on the space D[0,1] of functions with discontinuities only of the first kind. He defined a metric d on D[0,1] under which the space becomes a separable metric space and characterized the compact sets on (D[0,1],d). This opened the door for generalization of Donsker’s Invariance Principle. As the Skorokhod metric coincides with uniform metric on C[0,1], Donsker’s theorem can be derived from his work. However, Skorokhod soon produced an embedding theorem in stopped Brownian motion paths which allowed one to obtain Donsker’s Theorem easily. This is included in his book “Studies in the Theory of Random Processes”. In this book he also gives his approach to stochastic differential equations (SDE’s) driven by Lévy Processes. Using the Lévy-Itô decomposition, he shows that it is enough to study SDE’s driven by compensated Poisson Random measure and Brownian motion. Using an idea of I.I. Gikhman he gives existence of solutions to SDE’s with continuous coefficiencts. This was proven later by D. Stroock and S.R.S. Varadhan, who also proved the uniqueness of solution for the diffusion case. As this unique solution is Markov, their work advances the theory of PDEs. Their proof is non-trivial. Subsequently Gikhman and Skorokhod produced a proof based on Plancherel’s theorem, which can be extended to infinite dimensions. The work of Skorokhod using solutions for reflected diffusion using local time in the solution has led to major impacts.
Skorokhod left a great legacy with more than 50 students and numerous books in addition to basic contributions to Probability Theory including the Skorokhod integral and differentiation.
• Skorokhod, A.V. (1956) Limit theorems for stochastic processes, TPA, 2,
289-319.
• Obloj, J. (2004) Skorokhod embedding theorem and its offspring, Prob. Surveys,
1, 321-390.
• Gikhman, I.I. and Skorokhod, A.V. (1974) The theory of stochastic processes,
III, Springer.
• Mandrekar, V. and Skorokhod, A.V. (1998) An approach to Martingale problem for
diffusion stochastic equations in Hilbert-space. Theory of Stochastic Processes,
4, 54-59.
• Dupuis, P. and Ramanan, K. (1999) Convexity duality and Skorokhod Problem
I-II, PTRF, 115, 153-236.
Atmah Mandrekar, East Lansing
